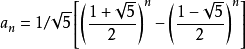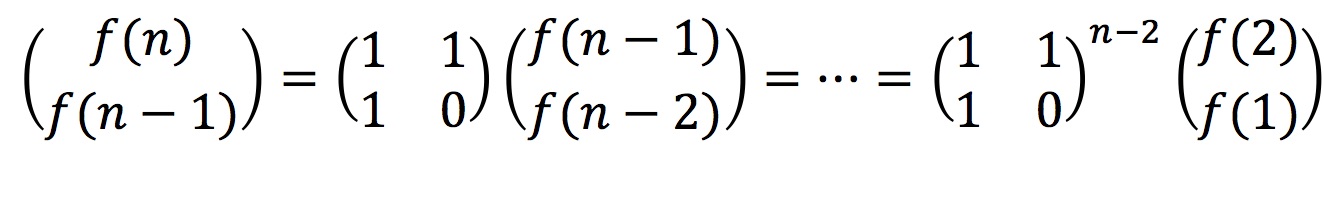1.定义及递推公式
斐波那契数列(Fibonacci sequence),又称黄金分割数列,因数学家Leonardoda Fibonacci以兔子繁殖为例子而引入,故又称兔子数列。
1,1,2,3,5,8,13…
即:f(1) = 1,f(2) = 1,f(3) = 2,f(4) = 3…
添加0项后,Fibonacci数列归纳如下:
- f(n) = f(n-1) + f(n-2), n >= 2;
- f(0) = 0;
- f(1) = 1;
2.通项公式
3.方法一:递归求解(时间复杂度O(2^n))
long fibonacci(unsigned n)
{
if (n < 2) return n;
return fibonacci(n-1) + fibonacci(n-2);
}
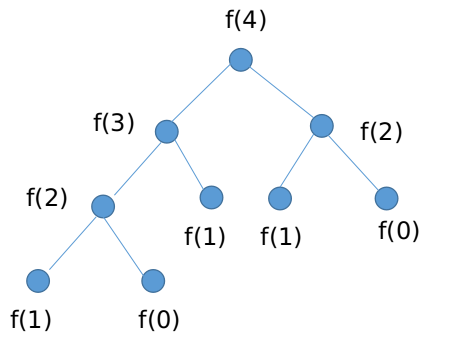
时间复杂度分析:可以看到,递归解法存在大量的重复计算。
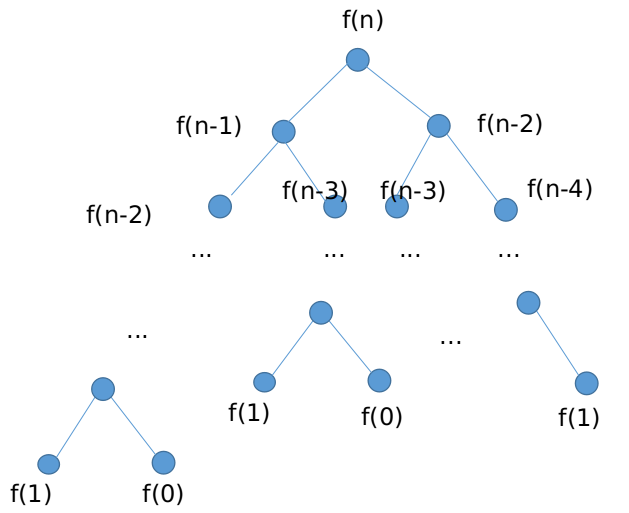
求f(n)的过程可以用一颗二叉树表示,树中的每个节点就代表一次基本计算.
易知,树的高度为n,一棵高度为n的满二叉树的节点个数为2^n-1,当然,上图中的树肯定不是满二叉树,但也可以看出来,该树的节点个数
大于满二叉树节点数的一半,即(2^n-1)/2。设计算次数为T(n),可知(2^n-1)/2 < T(n) < 2^n-1.
因此该算法的时间复杂度为O(2^n).
勘误 : 经评论提醒,关于斐波那契树的节点数说法有误,实际上,当n>4时,斐波那契树的节点数小于对应满二叉树的一半。我大致推算了一下,斐波那契树的节点数的计算也与斐波那契数列有关,准确的说,与斐波那契数列的和有关。
根据斐波那契树, 每个斐波那契数的出现次数如下所示:
1*f(n-1), 2*f(n-2), 3*f(n-3), 5*f(n-4), ..., f(n-1)*f(2), f(n)*f(1)
上式中的系数和即为斐波那契树的节点数之和。可以看出来,这些系数也是斐波那契数列,因此斐波那契树的节点数与斐波那契数列和有关。
而斐波那契数列是发散的,好像并没有求和公式,只有通项公式。不过通项公式与求和公式关系密切。
#设Sn为n阶斐波那契数列的和,则有如下公式:
Sn = f(n+2)-1
由通项公式方括号中的第一项,底数大约为1.6,第二项的底数为-0.6,n越大,第二项就越小,当n足够大,通项公式基本由第一项决定。那么,
可以推断,斐波那契树的节点数与1.6^n是同一数量级。也就是递归解法的时间复杂度为O(1.6^n), 而时间复杂度没有这种表示方法,进一步放大,就是O(2^n)。
4.方法二:利用动态规划(dp)求解(时间复杂度O(n))
long fibonacci_dp(unsigned n)
{
if (n < 2) return n;
long dp[n+1] = {0};
dp[0] = 0;
dp[1] = 1;
unsigned i = 2;
while(i<=n){
dp[i] = dp[i-1] + dp[i-2];
i++;
}
return dp[n];
}
显然,动态规划解法的时间复杂度为O(n).
5.方法三:利用矩阵求解(时间复杂度O(logn)
class Matrix
{
public:
unsigned n;
long **m;
Matrix(unsigned num)
{
m=new long*[num];
for (unsigned i=0; i<num; i++) {
m[i]=new long[num];
}
n=num;
clear();
}
void clear()
{
for (unsigned i=0; i<n; ++i) {
for (unsigned j=0; j<n; ++j) {
m[i][j]=0;
}
}
}
void unit()
{
clear();
for (unsigned i=0; i<n; ++i) {
m[i][i]=1;
}
}
Matrix operator=(const Matrix mtx)
{
Matrix(mtx.n);
for (unsigned i=0; i<mtx.n; ++i) {
for (unsigned j=0; j<mtx.n; ++j) {
m[i][j]=mtx.m[i][j];
}
}
return *this;
}
Matrix operator*(const Matrix &mtx)
{
Matrix result(mtx.n);
result.clear();
for (unsigned i=0; i<mtx.n; ++i) {
for (unsigned j=0; j<mtx.n; ++j) {
for (unsigned k=0; k<mtx.n; ++k) {
result.m[i][j]+=m[i][k]*mtx.m[k][j];
}
}
}
return result;
}
};
long fb_matrix(unsigned n) {
unsigned num=2;
Matrix first(num);
first.m[0][0]=1;
first.m[0][1]=1;
first.m[1][0]=1;
first.m[1][1]=0;
Matrix result(num);
result.unit();
unsigned t=n-2;
while (t) {
if (t%2) {
result=result*first;
}
first=first*first;
t=t/2;
}
return result.m[0][0]+result.m[0][1];
}
根据递推公式可以得到
因而计算f(n)就简化为计算矩阵的(n-2)次方,而计算矩阵的(n-2)次方,又可以分解为计算矩阵的(n-2)/2次方的平方,逐步分解,直到(n-2)/(2^m)==1,因而时间复杂度为O(logn).
matrix解法的时间复杂度为O(logn).
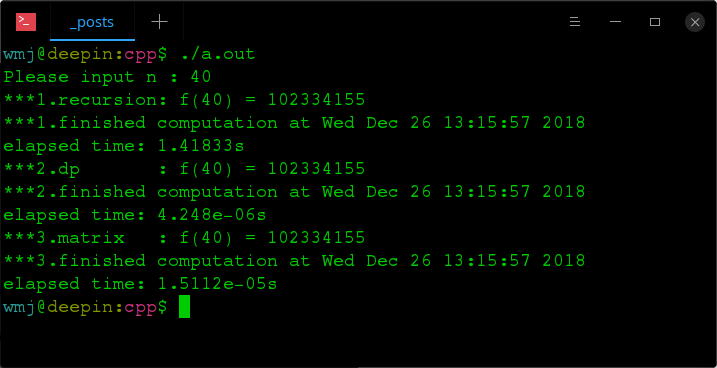
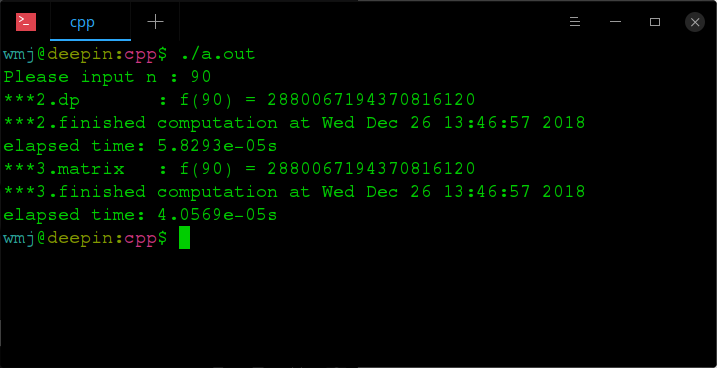
6.运行结果比较
- 可以看到,后两种解法比递归解法明显要快很多。
- 当n = 40时,动态规划解法比矩阵解法还要快些,都比递归解法快得多。
- 当n取更大些,比如n = 90时,动态规划解法就比矩阵解法慢了。